문제
요약
- 하노이탑 규칙
- 3개의 기둥이 있고, 첫 번째 기둥에 n개의 블록이 크기 순서대로 끼워져있다.
- 모든 블록은 자신보다 더 작은 블록 위로 올라갈 수 없다.
- 첫 번째 기둥의 모든 블록을, 세 번째 기둥으로 옮기면 된다.
분류
- 재귀
풀이
1. 내 풀이
- while 문을 이용한 풀이. 하노이탑을 그대로 배열로 시뮬레이션했다.
- n 을 1씩 늘려가면서, 모든 경우의 수를 따져보며 나만의 규칙을 도출했다.
- 옮길 블록을 f, 옮길 기둥의 가장 윗 블록을 t라고 하면, t - f 는 홀수여야 한다. (1순위)
- 1순위 탐색에 실패하면, 비어있는 기둥에 옮긴다.
from itertools import permutations as per
history = []
def solution(n):
arr = [[i for i in range(n , 0, -1)], [], []]
mod = n % 2
cur = 1
while len(arr[-1]) != n:
arr[2 if cur % 2 == mod else 1].append(arr[0].pop())
history.append([1, 3 if cur % 2 == mod else 2])
while len(arr[2 if cur % 2 == mod else 1]) != cur:
for f, t in per([0, 1, 2], 2):
if f == t or [t + 1, f + 1] == history[-1]: continue
if len(arr[f]) == 0 or len(arr[t]) == 0: continue
if (arr[t][-1] - arr[f][-1]) % 2 == 1 and arr[f][-1] < arr[t][-1]:
arr[t].append(arr[f].pop())
history.append([f + 1, t + 1])
break
else:
for f, t in per([0, 1, 2], 2):
if f == t or [t + 1, f + 1] == history[-1]: continue
if len(arr[f]) == 0: continue
if len(arr[t]) == 0:
arr[t].append(arr[f].pop())
history.append([f + 1, t + 1])
break
cur += 1
return history
2. 재귀 풀이
- 주어진 문제는 높이가 n인 탑을 첫 번째 기둥에서 세 번째 기둥으로 옮기는 것이다.
- 이는 높이가 n-1 인 탑을 두 번째 기둥으로 옮기는 것을 내포한다. n번째 블록을 세 번째 기둥에 놓은 후에는 높이가 n-1인 탑을 세 번째 기둥으로 옮겨야 한다.
- 높이가 n-2 인 탑은 세 번째 기둥으로 옮겨야 할 것이다. 그리고 세 번째 기둥에 있는 n-1 번째 블록 위로 옮겨야 한다.
- 이 과정을 n-k 가 1이 될 때까지 반복한다.
def hanoi(n, start, to, mid, answer):
if n == 1:
return answer.append([start, to])
hanoi(n - 1, start, mid, to, answer)
answer.append([start, to])
hanoi(n - 1, mid, to, start, answer)
def solution(n):
answer = []
hanoi(n, 1, 3, 2, answer)
return answer
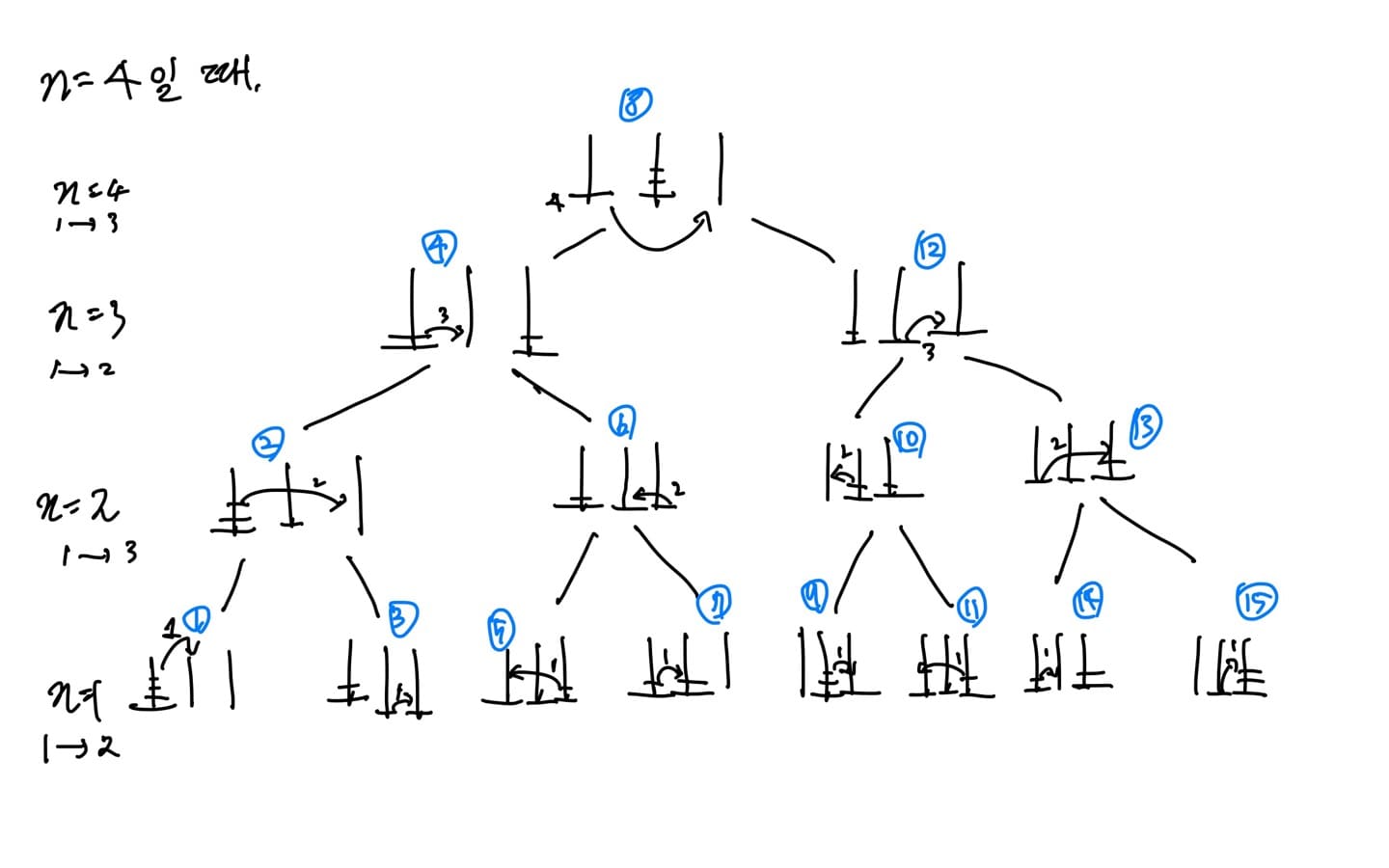
- 결국 재귀함수의 호출 양상은, 높이가 n 인 포화이진트리 구조를 띄게 된다.